ZX Spectrum Raytracer
This is the example output and source code for the 3rd iteration of the ZX Spectrum Raytracer, with shadows.
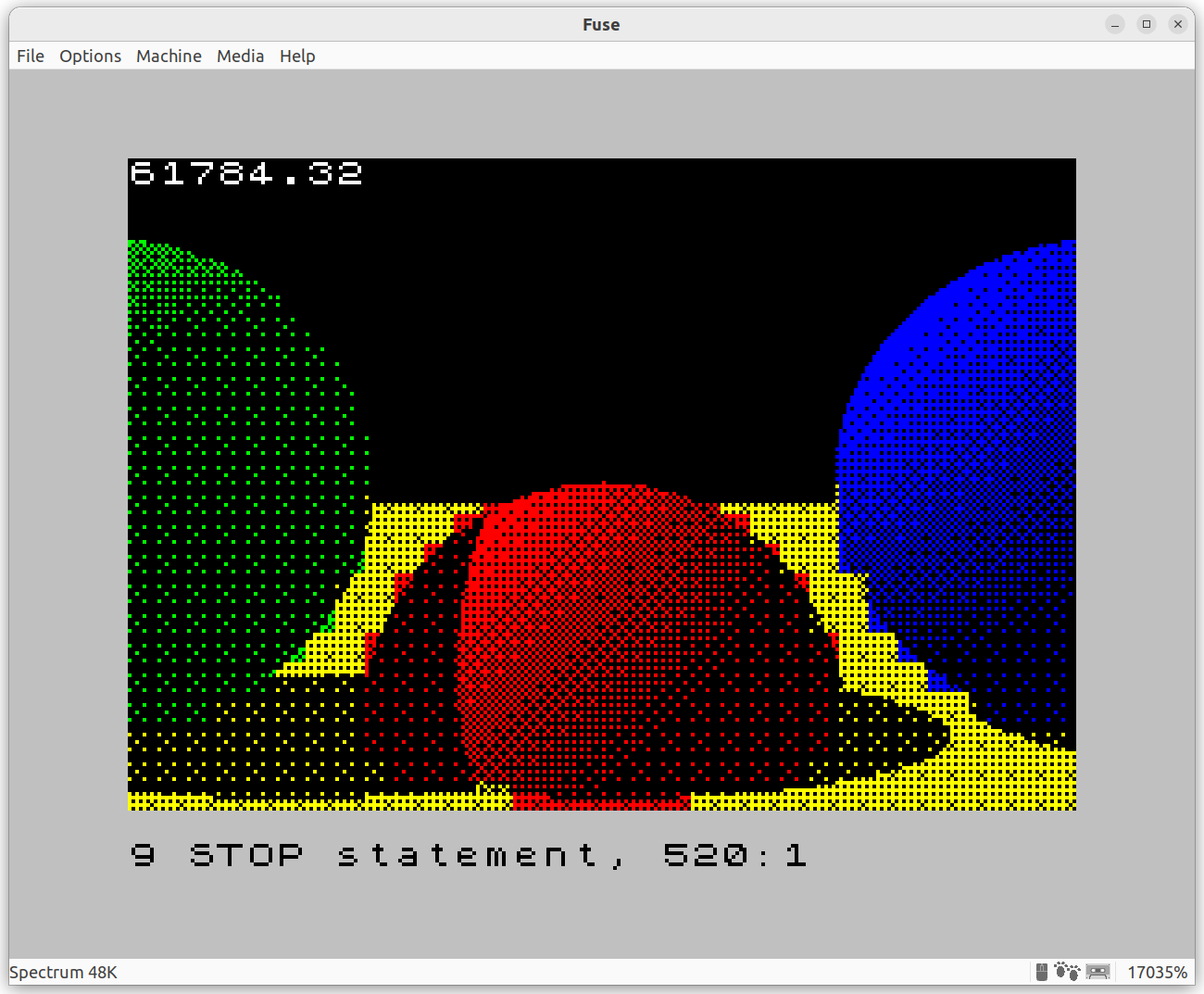
1 PAPER 0: INK 7: BRIGHT 1: CLS 2 GO SUB 8000 3 GO SUB 7000 4 DIM C(64): DIM L(64) 19 LET DZ = 1 20 FOR X = 0 TO 255 STEP 8 25 FOR Y = 0 TO 175 STEP 8 39 REM --- Fast approximate path: if all 4 corners of this 8x8 block black, ignore the block --- 40 LET DX = (X - 128) / 256: LET DY = (Y - 88) / 256: GO SUB 1000: LET CTL = PC: LET LTL = PL 41 LET DX = (X - 128 + 7) / 256: GO SUB 1000: LET CTR = PC: LET LTR = PL 42 LET DY = (Y - 88 + 7) / 256: GO SUB 1000: LET CBR = PC: LET LBR = PL 43 LET DX = (X - 128) / 256: GO SUB 1000: LET CBL = PC: LET LBL = PL 50 IF CTL = 0 AND CTR = 0 AND CBR = 0 AND CBL = 0 THEN GO TO 500 100 REM --- For each 8x8 block, collect the pixel colors and their counts --- 111 LET CI = 1 112 DIM A(8) 113 LET PL = 0 125 FOR U = X TO X+7 126 LET DX = (U - 128) / 256 130 FOR V = Y TO Y+7 140 IF CI = 1 THEN LET PC = CTL: LET PL = LTL: GO TO 160 141 IF CI = 8 THEN LET PC = CBL: LET PL = LBL: GO TO 160 142 IF CI = 57 THEN LET PC = CTR: LET PL = LTR: GO TO 160 143 IF CI = 64 THEN LET PC = CBR: LET PL = LBR: GO TO 160 150 LET DY = (V - 88) / 256 151 GO SUB 1000 160 LET A(PC+1) = A(PC+1) + 1 161 LET C(CI) = PC 162 LET L(CI) = PL 165 LET CI = CI + 1 170 NEXT V 171 NEXT U 199 REM --- Find most frequent color in this 8x8 block --- 201 LET MFC = 0 202 FOR C = 2 TO 8 203 IF A(C) > MFC THEN LET MFC = A(C): LET MFI = C 204 NEXT C 205 LET FC = MFI - 1 206 INK FC 300 REM --- PLOT the non-zero pixels if they're below the dithering threshold -- 301 LET CI = 1 310 FOR U = X TO X+7 311 FOR V = Y TO Y+7 320 IF C(CI) > 0 AND H(CI) <= L(CI) THEN PLOT U, V 325 LET CI = CI + 1 350 NEXT V 351 NEXT U 500 NEXT Y 505 GO SUB 3000: PRINT AT 0, 0; INK 7; TIME 510 NEXT X 520 STOP 990 REM ===== TraceRay ===== 991 REM Params: (DX, DY, DZ): ray direction 992 REM Returns: PC: pixel color; PL: pixel light intensity 993 REM Optimizations: ray origin hardcoded to (0, 0, 0); (TMIN, TMAX) hardcoded to (0, +inf) 994 REM Clobbers: A, CS, B, C, D, IX, IY, IZ, MT, NL, NX, NY, NZ, S, T 1000 LET MT = 1E10 1020 LET A = 2*(DX*DX + DY*DY + DZ*DZ) 1102 FOR S = 1 TO NS 1211 LET B = 2*(DX*S(S,1) + DY*S(S,2) + DZ*S(S,3)) 1212 LET C = (S(S, 1)*S(S, 1) + S(S, 2)*S(S, 2) + S(S, 3)*S(S, 3)) - S(S, 4) 1220 LET D = B*B - 2*A*C 1230 IF D < 0 THEN GO TO 1500 1231 LET D = SQR(D) 1240 LET T = (B + D) / A 1241 IF T > 0 AND T < MT THEN LET PC = S(S, 5): LET MT = T: LET CS = S 1250 LET T = (B - D) / A 1251 IF T > 0 AND T < MT THEN LET PC = S(S, 5): LET MT = T: LET CS = S 1500 NEXT S 1510 IF MT = 1E10 THEN LET PC = 0: RETURN 1600 LET IX = DX*MT: LET IY = DY*MT: LET IZ = DZ*MT 1601 LET NX = IX - S(CS, 1): LET NY = IY - S(CS, 2): LET NZ = IZ - S(CS, 3) 1610 LET PL = AI 1612 GO SUB 2100: IF H = 1 THEN RETURN 1615 LET NL = (NX*LX + NY*LY + NZ*LZ) 1620 IF NL > 0 THEN LET PL = PL + DI * NL / SQR(NX*NX + NY*NY + NZ*NZ) 2000 RETURN 2090 REM ----- Specialized TraceRay for shadow checks ----- 2091 REM Params: (IX, IY, IZ): ray start; (LX, LY, LZ): ray direction (directional light vector) 2092 REM Returns: H = 1 if the ray intersects any sphere, H = 0 otherwise 2093 REM Optimizations: (TMIN, TMAX) hardcoded to (epsilon, +inf) 2100 LET A = 2*(LX*LX + LY*LY + LZ*LZ) 2110 FOR S = 1 TO NS 2111 LET CX = IX - S(S,1): LET CY = IY - S(S,2): LET CZ = IZ - S(S,3) 2120 LET B = -2*(CX*LX + CY*LY + CZ*LZ) 2130 LET C = (CX*CX + CY*CY + CZ*CZ) - S(S, 4) 2140 LET D = B*B - 2*A*C 2150 IF D < 0 THEN GO TO 2210 2160 LET D = SQR(D) 2170 LET T = (B + D) / A 2180 IF T > 0.01 THEN LET H = 1: RETURN 2190 LET T = (B - D) / A 2200 IF T > 0.01 THEN LET H = 1: RETURN 2210 NEXT S 2220 LET H = 0: RETURN 2999 REM ===== Get timestamp in seconds ===== 3000 LET TIME = (65536*PEEK 23674 + 256*PEEK 23673 + PEEK 23672) / 50 3001 RETURN 6999 REM ===== Initialize 8x8 Bayer matrix ===== 7000 DIM H(64) 7001 RESTORE 7100 7002 FOR I = 1 TO 64 7003 READ H(I): LET H(I) = H(I) / 64 7004 NEXT I 7005 RETURN 7100 DATA 0, 32, 8, 40, 2, 34, 10, 42 7101 DATA 48, 16, 56, 24, 50, 18, 58, 26 7102 DATA 12, 44, 4, 36, 14, 46, 6, 38 7103 DATA 60, 28, 52, 20, 62, 30, 54, 22 7104 DATA 3, 35, 11, 43, 1, 33, 9, 41 7105 DATA 51, 19, 59, 27, 49, 17, 57, 25 7106 DATA 15, 47, 7, 39, 13, 45, 5, 37 7107 DATA 63, 31, 55, 23, 61, 29, 53, 21 7999 REM ===== Initialize scene ===== 8000 LET LX = -1/SQR(2): LET LY = 1/SQR(2): LET LZ = 0: LET AI = 0.075: LET DI = 1 - AI 8010 RESTORE 9000 8011 READ NS 8012 DIM S(NS, 5) 8020 FOR S = 1 TO NS 8021 FOR I = 1 TO 5 8022 READ S(S, I) 8030 NEXT I 8031 NEXT S 8040 RETURN 8998 REM ----- Sphere data ----- 8999 REM Sphere count, followed by (CX, CY, CZ, SR*SR, SC) 9000 DATA 4 9001 DATA 0, -1, 4, 1, 2 9002 DATA 2, 0, 4, 1, 1 9003 DATA -2, 0, 4, 1, 4 9004 DATA 0, -5001, 0, 5000^2, 6